Deducción de la Fórmula General de la Cuadrática (para niños)
¿Se acuerdan de la famosa solución de la cuadrática?
Esta, sí, esta vaina:
Recuerdo que cuando me la enseñaron en primaria, nada más los profesores decían que teníamos que aprendernos la fórmula pasa sacar las dos posibles respuestas para x a partir de la dichosa formulita de la cuadrática. Una vez le pregunté al profesor – “¿y esa fórmula de dónde sale?” el viejo me dijo que dejara de preguntar y que mejor me la aprendiera, entonces me fui a preguntarle a mi mamá, que por cierto es Licenciada en Matemáticas, entonces ella me explicó el porqué de la puta fórmula.
Recordemos un poco las tonteras del colegio, si se relaciona la ecuación de segundo grado con un polinomio de segundo grado y las raíces del mismo (a su vez raíces de una función cuadrática), entonces podemos resolver la ecuación algebraicamente y de esta forma obtener la fórmula de dicha ecuación. Para esta fórmula hay varias soluciones, está la de Cardano – Viete y la de cambio de variable, pero nosotros nos vamos a ir por la solución más usada.
Sea dada la ecuación:
Ahora la explicación:
Al resolver ecuaciones de segundo grado de la forma
completando el cuadrado realizamos lo siguiente:
a)
Sumar – c a cada lado de la ecuación:
Creo que no necesito explicar el porqué de la resta de – c, ¿O, sí? Por si acaso, aquí va:
y queda:
b)
Dividir cada ladoa
Donde
Para garantizar que sea realmente una ecuación polinómica de segundo grado. Como a es distinto de cero, entonces sí podemos dividir entre a cada término de la ecuación:
Se anulan las a:
Y queda:
c)
Se observa que hay un trinomio cuadrado perfecto incompleto, falta el tercer miembro. Para completar el trinomio cuadrado perfecto (TCP), o brevemente, para completar el cuadrado en el miembro izquierdo, se toma en cuenta la regla que "el cuadrado del primero más el doble producto del primero por el segundo más el segundo al cuadrado",
¿Qué le falta a cada lado para ser equivalente?, entonces sería:
Ahora este se pone a ambos lados, así:
Los términos son equivalentes:
d) )
Para que sea más fácil podemos hacer por separado las operaciones de ambos lados, o operar primero una parte e ir bajando su resultado a medida se va resolviendo el otro lado, o puede hacerlo simultáneamente.
En este caso, sumar las fracciones de lado derecho de la ecuación tomando como MCD 4a2
Factorizamos el lado izquierdo:
Hacemos la operación con fracciones en el miembro derecho y queda esto:
e)
Simplificar y extraer la raíz de ambos miembros (¡Uy!)
f)
Despejamos la incógnita que buscamos, que es x:
Y nos queda:
¡¡¡Vaya!!! ¡¡¡De aquí sale esta vaina!!!
Consideraciones:
Si b2 –4ac es mayor que cero, hay dos soluciones
Si b2 –4ac es igual a cero hay una solución
Si b2 –4ac es menor que cero, no hay solución
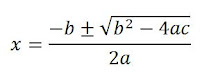








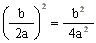










Comentarios
Gracias y saludos.
Víctor Amado H.
Saludos